基于法拉第電磁感應(yīng)理論的電磁流量計(jì)已經(jīng)廣泛應(yīng)用到流量測(cè)量中 。其中權(quán)函數(shù)的研究對(duì)分析電磁流量計(jì)是非常重要和必不可少的。它說(shuō)明了，在同一管道橫截面上，各點(diǎn)流速對(duì)電極信號(hào)的貢獻(xiàn)不同，遵循一定的分布 。傳統(tǒng)的電磁流量計(jì)具有絕緣的測(cè)量管壁，或者內(nèi)壁附有一層絕緣材料  。其權(quán)函數(shù)的解析解表明權(quán)值在圓心處為 １ ，在圓周 （除電極外）為 ０．５ ，在電極附近最大 。但很多情況下，測(cè)量管壁并不是絕緣的或者管壁被污染而變成非絕緣性。典型例子就是血液電磁流量計(jì)測(cè)量中把血管壁視為絕緣，實(shí)際上血管壁是非絕緣的 。但迄今為止，針對(duì)非絕緣管壁電磁流量計(jì)權(quán)函數(shù)的研究仍然很少。這就造成了實(shí)際應(yīng)用中出現(xiàn)很多問題。如在醫(yī)學(xué)中，更好的利用電磁流量計(jì)來(lái)測(cè)量血液流速；在工業(yè)中，怎樣研究測(cè)量管壁或者電極被污染給測(cè)量帶來(lái)的影響。

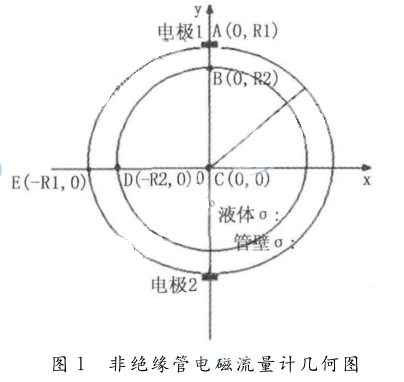
２　 非絕緣管電磁流量計(jì)權(quán)函數(shù)分析

２．１　 利用拉普拉斯方程求解權(quán)函數(shù)絕緣管電磁流量計(jì)是借助格林函數(shù)解拉普拉斯方程得到權(quán)函數(shù)的解析解 。

         歐姆定律：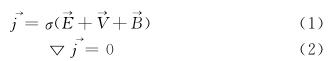

 

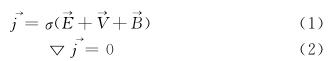
        將式 （ １ ）代入式 （ ２ ），得到電磁流量計(jì)的基本微分方程：

 

         電導(dǎo)率均勻則有：

 

         借用格林函數(shù)，得到絕緣管壁電磁流量計(jì) （長(zhǎng)管）的解析解 ：

 

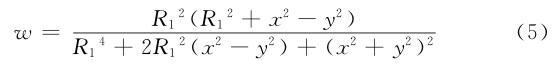
        Ｒ １ 為絕緣管的半徑。但是對(duì)于非絕緣管壁方程 （ ４ ）不成立，這是因?yàn)楣鼙诘碾妼?dǎo)率與管內(nèi)液體電導(dǎo)率不等。對(duì)于方程（ ３ ）很難利用解偏微分方程來(lái)得到非絕緣管壁的電磁流量計(jì)權(quán)函數(shù)。

 

２．２　 利用虛電流密度分布得到權(quán)函數(shù)分布權(quán)函數(shù) ：

 

         模型中，電極可視為點(diǎn)電極。內(nèi)壁上與之相對(duì)應(yīng)點(diǎn) Ｂ （如圖１）的虛電流密度為 （ ０＜ ｊ ＜１ ），其在非絕緣管道上的投影為：

 

 

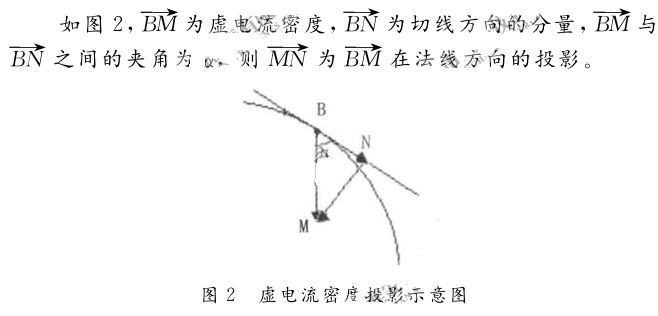
        由歐姆定律可知：

 

         其中： σ １ 為管壁的電導(dǎo)率。

 

        那么 Ａ 點(diǎn)的電場(chǎng)強(qiáng)度：

 

        將式 （ ８ ）、（９ ）代入式 （ ７ ）得到非絕緣管壁上任意點(diǎn)的電流密度：

 

        虛電流與 σ １ 成正比，與 ｈ 成反比。